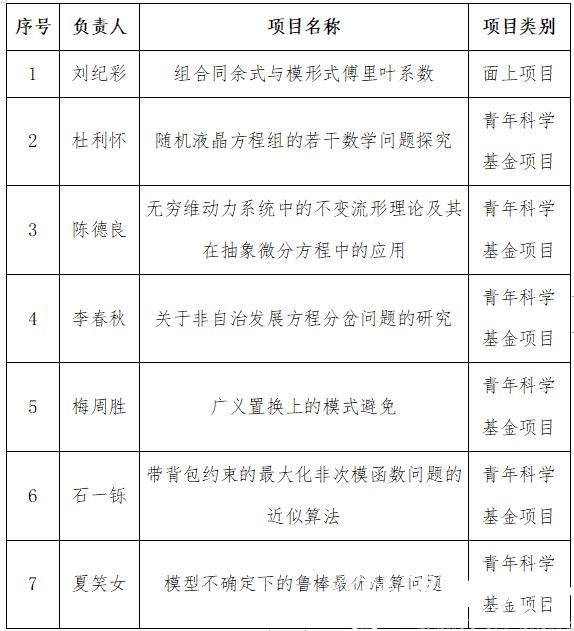
新学期即将开始，近日，国家自然科学基金委公布2021年度国家自然科学基金立项结果，温州大学数理学院再创佳绩，喜获七项国家自然科学基金项目，其中面上项目1项，青年科学基金项目6项，凸显了我院教师扎实的科研实力和优异的学术水平，特向广大师生、校友报喜！

延伸阅读：

姓名：刘纪彩

研究方向：组合数论

立项项目：组合同余式与模形式傅里叶系数

项目简介：组合同余式是组合数学近些年的一个研究热点，并且吸引了很多国内外学者利用不同的方法来研究它们，获取新的组合同余式往往能够推动组合数学、符号计算与特殊函数论等研究方向的发展。特别地，涉及模形式傅里叶系数的组合同余式是组合数论中的一个难点，并且这类组合同余式与组合恒等式、符号计算、p-adic分析、特殊函数论、椭圆曲线、Calabi–Yau流形等研究领域紧密相关，研究这类组合同余式具有非常重要的意义。该项目将利用组合恒等式、超几何级数变换公式、p-adic Gamma函数、以及Gauss和来研究若干个与模形式傅里叶系数相关的超同余式，为截断超几何级数与模形式傅里叶系数之间的关系研究提供更多的理论依据。

姓名：杜利怀

研究方向：随机偏微分方程

立项项目：随机液晶方程组的若干数学问题探究

项目简介：本项目将运用调和分析、半经典分析以及随机分析等现代分析技术，对随机液晶方程组展开系统性的研究。具体来说，我们将研究(1)液晶方程组关于低正则随机初值弱解的整体存在性和唯一性；(2)随机液晶方程组在临界空间解的局部存在性和整体存在性；(3)白噪对解的正则性效应；(4)不变测度的存在性和遍历性。本项目的研究成果有望进一步地完善随机流体方程的理论，同时对液晶的实际应用提供理论指导。

姓 名：陈德良

研究方向：无穷维动力系统

立项项目：无穷维动力系统中的不变流形理论及其在抽象微分方程中的应用

项目简介：本项目主要研究无穷维动力系统中部分法向双曲不变流形理论以及几类适定和非适定微分方程不变流形和不变叶层理论。由于在某些偏微分方程中不变流形的双曲性不满足法向双曲性以及受到双曲动力系统自身理论的影响，近年来部分法向双曲性受到来自偏微分方程和动力系统等方向专家的关注。我们拟研究Banach空间中一类抽象的“广义”动力系统在满足部分法向双曲性的近似不变流形或不变紧集附近局部不变流形的存在性和正则性，并给出一些应用；同时，我们还预期将丛上动力系统的不变图和不变叶层理论应用于某几类适定和非适定抽象微分方程。

姓 名：李春秋

研究方向：动力系统

立项项目：关于非自治发展方程分岔问题的研究

项目简介：本项目拟从吸引子和不变集分岔的角度研究非自治发展方程分岔理论及其应用方面的问题。对非自治系统主算子依赖或不依赖于时间的情况下，分别建立其局部不变集（吸引子）分岔定理和无穷远不变集分岔等方面结果，并给出具体的应用。

姓 名：梅周胜

研究方向：计数组合

立项项目：广义置换上的模式避免

项目简介：模式避免问题是当前计数组合的研究热点之一。置换与重集置换上模式避免的研究日趋完备，广义置换是置换与重集置换的统一与推广，其上的相关研究才刚开始。前期我们在广义置换上引入了模式避免的概念，借助RSK算法和Young表的性质将Knuth在置换上的经典结果延伸到了广义置换，即3长模式在广义置换中仅形成一个Wilf-等价类。在此基础上，本项目将从Wilf-等价类的划分与计数、模式避免与Young 表、统计量三个方面进一步研究广义置换上模式避免。主要研究内容包括：系统研究3长模式集在广义置换上Wilf-等价类的划分与相关计数；研究计数Young表的Kostka数的Schur-凹性与极值结构，进一步挖掘RSK算法与Young表在模式避免问题中的更多应用；探索广义置换上逆序数、下降数、主指标这三个统计量的定义和生成函数，研究广义置换关于其type的生成函数的对称性。本项目的开展将对统一和完善置换与重集置换上模式避免的研究有着重要意义。

姓 名：石一铄

研究方向：社会网络、通讯网络中组合优化问题的近似算法

立项项目：带背包约束的最大化非次模函数问题的近似算法

项目简介：本项目拟研究带背包约束的最大化非次模函数(MnsK)问题以及其相关问题的计算复杂性和近似算法。MnsK问题的目标是找到一个子集，使得该子集的非次模目标函数值最大，同时满足子集中每个元素的费用之和不超过预算。本项目旨在缩小具体MnsK问题的不可近似性和近似比间隙，设计在目标函数为非单调情况下的近似算法，以及进一步研究目标函数为非单调可取负值情况下的近似算法。

姓 名：夏笑女

研究方向：金融数学、随机控制、投资组合最优清算

立项项目：模型不确定下的鲁棒最优清算问题

项目简介：传统金融理论的一个重要假设就是市场无摩擦，然而在现实的金融市场中，机构投资者的大额交易往往会产生额外的价格冲击成本。近年来，考虑冲击成本的投资组合清算问题在金融数学和随机控制领域中引起了广泛的关注。这类问题的主要特征是由清算约束引起的值函数奇异终端条件，转化到对应的Hamilton-Jacobi-Bellman（HJB）方程上则会产生奇异终端约束。本项目拟研究证券基准价格或价格冲击参数的不确定性对于清算模型中的最优交易策略的影响。我们首先考虑驱动价格冲击参数的扩散过程存在不确定跳跃的鲁棒清算问题，然后考虑证券基准价格的漂移项只有部分信息下的鲁棒清算问题。